Noncentral F-distribution
In probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the (ordinary) F-distribution. It describes the distribution of the quotient (X/n1)/(Y/n2), where the numerator X has a noncentral chi-squared distribution with n1 degrees of freedom and the denominator Y has a central chi-squared distribution n2 degrees of freedom. It is also required that X and Y are statistically independent of each other.
It is the distribution of the test statistic in analysis of variance problems when the null hypothesis is false. The noncentral F-distribution is used to find the power function of such a test.
Contents |
Occurrence and specification
If  is a noncentral chi-squared random variable with noncentrality parameter
is a noncentral chi-squared random variable with noncentrality parameter  and
and 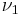 degrees of freedom, and
degrees of freedom, and  is a chi-squared random variable with
is a chi-squared random variable with 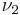 degrees of freedom that is statistically independent of
degrees of freedom that is statistically independent of  , then
, then
is a noncentral F-distributed random variable. The probability density function for the noncentral F-distribution is [1]
when 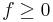 and zero otherwise. The degrees of freedom
and zero otherwise. The degrees of freedom 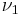 and
and 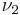 are positive. The noncentrailty parameter
are positive. The noncentrailty parameter  is nonnegative. The term
is nonnegative. The term 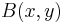 is the beta function, where
is the beta function, where
The cumulative distribution function for the noncentral F-distribution is
where  is the regularized incomplete beta function.
is the regularized incomplete beta function.
The mean and variance of the noncentral F-distribution are
and
Special cases
When λ = 0, the noncentral F-distribution becomes the F-distribution.
Related distributions
Z has a noncentral chi-squared distribution if
where F has a noncentral F-distribution.
Implementations
The noncentral F-distribution is implemented in the R language (e.g., pf function), in MATLAB (ncfcdf, ncfinv, ncfpdf, ncfrnd and ncfstat functions in the statistics toolbox) in Mathematica (NoncentralFRatioDistribution function), in NumPy (random.noncentral_f), and in Boost C++ Libraries.[2]
A collaborative wiki page implements an interactive online calculator, programmed in R language, for noncentral t, chisquare, and F, at the Institute of Statistics and Econometrics, School of Business and Economics, Humboldt-Universität zu Berlin.[3]
Notes
- ^ S. Kay, Fundamentals of Statistical Signal Processing: Detection Theory, (New Jersey: Prentice Hall, 1998), p. 29.
- ^ John Maddock, Paul A. Bristow, Hubert Holin, Xiaogang Zhang, Bruno Lalande, Johan Råde. "Noncentral F Distribution: Boost 1.39.0". Boost.org. http://www.boost.org/doc/libs/1_39_0/libs/math/doc/sf_and_dist/html/math_toolkit/dist/dist_ref/dists/nc_f_dist.html. Retrieved 20 August 2011.
- ^ Sigbert Klinke (10 December 2008). "Comparison of noncentral and central distributions". Humboldt-Universität zu Berlin. http://mars.wiwi.hu-berlin.de/mediawiki/slides/index.php/Comparison_of_noncentral_and_central_distributions.
References
- Weisstein, Eric W., et al. "Noncentral F-distribution". MathWorld. Wolfram Research, Inc. http://mathworld.wolfram.com/NoncentralF-Distribution.html. Retrieved 20 August 2011.
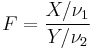
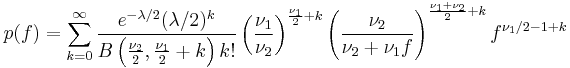
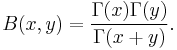
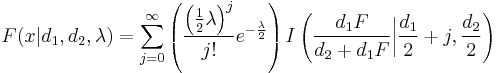
![\mbox{E}\left[F\right]=
\begin{cases}
\frac{\nu_2(\nu_1%2B\lambda)}{\nu_1(\nu_2-2)}
&\nu_2>2\\
\mbox{Does not exist}
&\nu_2\le2\\
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/8eece4bb39033214ed7e2fe7ecbd6c93.png)
![\mbox{Var}\left[F\right]=
\begin{cases}
2\frac{(\nu_1%2B\lambda)^2%2B(\nu_1%2B2\lambda)(\nu_2-2)}{(\nu_2-2)^2(\nu_2-4)}\left(\frac{\nu_2}{\nu_1}\right)^2
&\nu_2>4\\
\mbox{Does not exist}
&\nu_2\le4.\\
\end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/71a684c4f5d74b45f15d453b34b7163f.png)